Modelowanie zbijania się pingwinów cesarskich w gromadę: każdy dostaje równie dużo ciepła

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0050277

Oto założenia autorów:

1. Pingwiny tworzą formację i są ściśnięte w gromadę w najbardziej wydajny sposób: heksagonalnie. (To odpowiada temu, jak wydają się skupiać w taką gromadę w naturze.)
2. Zakłada się, że pingwiny zbijają się w gromadę na płaszczyźnie i są tych samych rozmiarów i kształtów. Wieje wiatr.
3. Pingwiny doznają założonej utraty ciepła z tymi, które są na zewnątrz formacji, tracącymi więcej ciepła.

Następnie autorzy wykonują symulację, w której zmarznięte pingwiny przesuwają się po jednym, żeby się ogrzać. Oto kroki, które symulują:

1. Stworzenie zbitej gromady i ustalenie jej granic.
2. Wyliczenie siły wiatru wiejącego wokół gromady.
3. Wyliczenie profilów temperatury wokół gromady.
4. Wyliczenie lokalnej utraty ciepła dla każdego pingwina.  
5. Dodanie losowego zróżnicowania tempa utraty ciepła (fakultatywne).
6. Zidentyfikowanie pingwina o najwyższym tempie utraty ciepła (“wędrowca”) i przesunięcie go do granicy miejsca, gdzie utrata ciepła jest najmniejsza.
7. Ustalenie nowej granicy gromady.
8. Powtórzenie pożądaną ilość razy przez powrót do kroku 2.  

“Quanta” pokazuje diagram, jak działa symulacja:

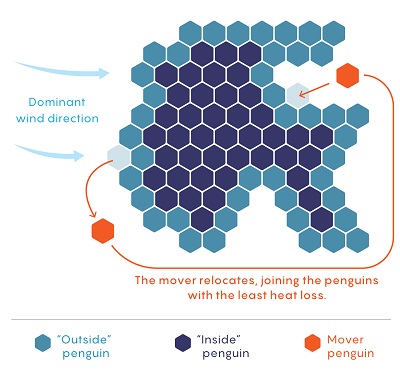
Zauważycie natychmiast, że niektóre z tych założeń są zbyt uproszczone – szczególnie to, że najbardziej zmarznięty pingwin jest tym, który wędruje i przechodzi do najcieplejszego miejsca na peryferii, nie zaś tylko do cieplejszego. Wideo gromady powyżej nie wydaje się pokazywać tylko jednego pingwina, który się przesuwa, ani też nie wydaje się realistyczne, by wędrowiec od razu znalazł najcieplejsze możliwe miejsce. Proszę zauważyć jednak, że kiedy przesuwa się najbardziej zmarznięty pingwin, wewnętrzny pingwin staje się zewnętrznym pingwinem i to tworzy nowego wędrowca i tak dalej. W końcu kształt gromady zmienia się.

Jak pokazuje poniżej diagram z artykułu, model pokazuje, że gromada zmienia się z nieregularnej na z grubsza prostokątną z jedną krótszą stroną prostokąta naprzeciwko wiatru. (Krótsze strony prostokąta są zaokrąglone, nie zaś proste.) Po około 50 powtórkach modelu zaczyna wyłaniać się stały kształt. Tutaj jest diagram z artykułu, pokazujący zmianę kształtu w czasie (po powtórkach) z wiatrem wiejącym z lewej strony.

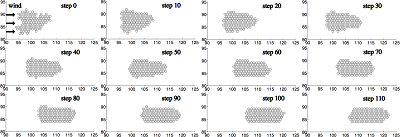
Interesującym wynikiem tego modelu jest to, że w ostatecznym rachunku wszystkie pingwiny doświadczają mniej więcej tej samej utraty ciepła i mają z grubsza równy dostęp do ciepła wewnątrz gromady. To jest przykład samolubnego zachowania, które daje równość ciepła dla wszystkich. Autorzy notują także, że model nie daje najmniejszej utraty ciepła dla kolonii jako całości, która moim zdaniem wynikałaby z koła. (Tylko zgaduję.)

Wartość symulacji jest tylko tak dobra, jak jej moc przewidywania. Czy pingwiny zbijają się w gromady rzeczywiście przyjmując z czasem te kształty? Odpowiedź wydaje się brzmieć: niezbyt: nie są to wydłużone prostokąty, ale bardziej nieregularne kształty. (Jedna prognoza, która była jednak potwierdzona poprzednio, to że pingwiny są upakowane heksagonalnie.)

Autorzy “podkręcili” model przez pozwolenie na losowe zróżnicowanie utraty ciepła przez poszczególne pingwiny, co daje bardziej nieregularne kształty i, jak piszą autorzy, dają kształt gromady “jakościowo podobne do rzeczywistych gromad”. Wskazują na ilustrację, która ma pokazywać jakościowe podobieństwo (Ilustracja 5a), ale tego nie pokazuje: pokazuje, że gromady stają się bardziej nieregularne w kształtach, kiedy wzrasta stopień losowych zakłóceń. Byłoby lepiej, gdyby pokazali kilka rzeczywistych kształtów gromad, ewoluujących z czasem.  

Artykuł w “Quanta” nawiązuje do badań o utracie ciepła i ruchach pingwinów, które są w toku i mogą z czasem dać jakieś dane, ale jeszcze ich nie ma. Dane pokazują jednak, jak przewidywano, że jednostki mają tendencję do przesuwania się z nawietrznej na zawietrzną stronę gromady i że ten ruch jest wyraźniejszy przy silniejszych wiatrach.  

Wiele pozostaje do zrobienia, włącznie z obserwacjami kolonii, żeby zobaczyć, jak przesuwają się poszczególne pingwiny. Jest to jednak bardzo trudne przy okropnych warunkach pogodowych i problemach z umieszczaniem naukowców koło tych narażonych kolonii. (Jeden z cytowanych artykułów zawiera opis zdalnie sterowanego obserwatorium.) I, oczywiście, jeśli założenia modelu okażą się błędne, jak wydaje się być parę z nich, to model wymaga poważnego przebudowania. Przynajmniej jednak autorzy wyodrębnili zgrabny problem, który może mieć dość proste rozwiązanie. Sądzę jednak, że rozwiązanie będzie musiało dotyczyć więcej niż jednego pingwina poruszającego się równocześnie!

h/t: Paul

_________

Article Source:Waters A, Blanchette F, Kim AD (2012) Modeling Huddling Penguins. PLOS ONE 7(11): e50277. https://doi.org/10.1371/journal.pone.0050277

Modeling the huddling behavior of Emperor penguins: everybody gets equal warmth

Why Evolution Is True, 18 sierpnia 2020

Tłumaczenie: Małgorzata Koraszewska